Solteorien hos Ptolemaios
Tilbage til indholdSolteorien er helt klart ikke Ptolemaios’ eget værk. Han bygger på Hipparch (ca. 190 - ca. 120 f.Kr.) og Apollonius (ca. 262 - ca. 190 f. Kr.). Men deres arbejde er først og fremmest kendt gennem Ptolemaios.
Formålet med solteorien skal være at opbygge en geometrisk model, hvis parametre bestemmes ved hjælp af observationer, på en sådan måde, at den kan forudsige de karakteristiske egenskaber ved Solens bevægelse - først og fremmest dens varierende hastighed i årets løb.
I Almagesten behandles solteorien i Bog III Kap. 18
Den første opgave må være at bestemme årets længde. Ptolemaios nævner to måder at definere årets længde på - med moderne termer: det tropiske år og det sideriske år.
Det tropiske år forklares som tidsrummet for Solens tilbagevenden til samme solhverv eller samme jævndøgn. Således kobles Solens tilsyneladende bevægelse langs ekliptika med årstiderne. Hvis denne bevægelse beskrives med den ekliptiske længde l ¤ (t) af solcentret, regnet fra forårspunktet ^ , hvor Solen ses ved forårsjævndøgn, vil vi opleve starten af
| foråret | når l ¤ (t) = | 0° |
(forårsjævndøgn) | |||
| sommeren | når l ¤ (t) = | 90° |
(sommersolhverv) | |||
| efteråret | når l ¤ (t) = | 180° |
(efterårsjævndøgn) | |||
| vinteren | når l ¤ (t) = | 270° |
(vintersolhverv) |
Det skal bemærkes, at der er tale om de astronomiske årstider! Ptolemaios argumenterer for, at det er det tropiske år, der skal bruges i solteorien. For kun på den måde kan man opretholde sammenhængen mellem de skiftende årstider og tidspunktet på året.
Han kender også - bl. a. gennem Hipparch - det sideriske år. Det er tidsrummet mellem to af Solens passager af en bestemt stjerne (kan ikke observeres!), og det angives i Almagesten til lidt længere end 365,25 døgn.
Helt præcist bestemmes det tropiske års længde. Ptolemaios gengiver først Hipparchs resultat, der bygger på "gamle" observationer; derpå sammenligner han egne observationer med de gamle og når til samme resultat. Dvs.
det tropiske år er konstant,
og
1 tropisk år = 365 + ¼ - 1/300 døgn
= 365d;14,489
= 365d5h55m12s 10
Den moderne værdi er 365d5h48m46s, så der er tale om et ganske godt resultat.
Dette resultat følges nu op af følgende afsnit, der kan opfattes som Ptolemaios’ program for resten af værket:
Was aber die für die Sonne und die anderen Gestirne erforderliche Bestimmung ihres jeweiligen Laufs anbelangt, für welche das Handbuch in Form spezieller Tabellen handliche und sozusagen zum Gebrauch fertige Unterlagen zu bietet hat, so wird wir zwar der Meinung, daß für den Mathematiker das Endziel seiner Aufgabe in dem Nachweis bestehen muß, daß die Erscheinungen am Himmel sich alle infolge gleichförmiger und auf Kreisen vor sich gehender Bewegungen vollziehen, indessen gehört unseres Erachtens zu diesem schwierigen Vorhaben als notvendige Beigabe unbedingt die Aufstellung von Tafeln, welsche zunächst die Teilbeträge der gleichförmigen Bewegung (Kap. 2) getrennt zeigen von der scheinbaren Anomalie (Kap. 6), die bei der Annahme von Kreisen eintritt, und dann wieder aus der Mischung und Vereinigung dieser beiden Bewegungen (Kap. 8) den Nachweis des scheinbaren Laufs der Gestirne ermöglichen11.
Platons ide om at benytte jævne cirkelbevægelser i modellerne fastholdes, og første opgave bliver at opstille tabeller over Solens middelbevægelser i 18 års perioder, 1 års perioder, 30 døgns perioder, 1 døgns perioder og 1 times perioder12.
Ptolemaios beregner tabellerne ved hjælp af størrelsen
w ¤ = 360° /365;14,48 = 0° ;59,8,17,13,12,31 pr. døgn. ( 1)
Den repræsenterer det antal grader, Solen ville flytte sig pr. døgn i ekliptika, hvis dens bevægelse havde været jævn.
Situationen kan også i stedet opfattes på den måde, at vi indfører en middelsol i ekliptika som et punkt, der flytter sig med jævn hastighed på ekliptika og gennemfører netop ét omløb i løbet af ét tropisk år. Middelsolens længde skal så beregnes som
l m(t) = l m(to) + w ¤ (t - to) ( 2)
hvor er et begyndelsestidspunkt - epoke - som senere vælges.
Når Ptolemaios så skal tage højde for, at Solen faktisk bevæger sig ujævnt i ekliptika, har han to tidligere, græske modeller at arbejde med.
Den excentriske model tilskrives Hipparch
Med vektornotation gælder følgende
![]() =
= ![]()
De tre vektorer ligger i ekliptikas plan. Solen P antages at bevæge sig mod øst med konstant vinkelhastighed w ¤ på en excentrisk cirkel med radius R og centrum D, som ligger uden for jordens centrum T i en afstand TD = e (excentriciteten). P gennemløber deferenten i løbet af ét tropisk år.
Figur 2 Den excentriske model |
Set fra T vil P bevæge sig med varierende vinkelhastighed. Men modellen
fører altså denne anomali (afvigelse) tilbage til en jævn cirkelbevægelse i
overensstemmelse med Ptolemaios’ program. TD’s retning ligger fast og er rettet mod solbanens apogæum A, som projiceres på ekliptika i punktet A*, som har længden l a regnet fra forårspunktet ^ 13. |
Epicykel modellen tilskrives Apollonius
Med vektornotation gælder følgende
![]() =
= ![]()
For at denne model kan give præcis samme retning fra T til P og samme afstande mellem de to steder, som den excentriske model leverer, kræves blot
CP er lig med og parallel med TD
TC er lig med og parallel med DP
| Det betyder geometrisk, at P vil bevæge sig med konstant vinkelhastighed w ¤ mod vest på
en cirkel (epicyklen) med centrum C og radius r = e samtidig med, at centret C bevæger
sig med konstantvinkelhastighed w ¤ mod øst på en cirkel (deferenten) med centrum i
Jordens centrum og radius R14. Igen vil P - set fra T - bevæge sig med varierende vinkelhastighed. Men modellen fører igen denne anomali (afvigelse) tilbage til jævne cirkelbevægelser i overensstemmelse med Ptolemaios’ program. |
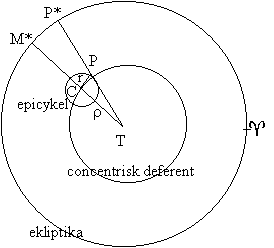 Figur 3 Epicykel modellen |
Ptolemaios viser omhyggeligt, at de to modeller stemmer overens - både i tilfælde af, at længderne CP = r = TD = e samtidig med, at længderne TC = r = DP = R15 og i tilfælde af, at r /r = R/e samtidig med, at r ¹ R16. Altså vil de give identiske løsninger!
Man skulle så mene, at Ptolemaios passende kunne beslutte sig for den ene model, og så holde sig til den alene. Han vælger senere den excentriske model17 med den begrundelse, at den er enklere, idet den fører til målet ved kun at benytte én cirkelbevægelse i modsætning til epicykel modellen, som benytter to. Men han gennemfører næsten alle beviser og beregninger i begge modeller! Her vil vi holde os til den excentriske model.
For at vi i detaljer kan opstille den excentriske model for Solens bevægelse, må vi have indført nogle variable, som kan fastlægge modellens udseende til et vilkårligt tidspunkt. Vi kan anvende to systemer af parametre - det ene i forhold til forårspunktet, ^ , det andet i forhold til den excentriske cirkels apogæum18.
Vi har allerede indført Solens middellængde l m(t) i formel (1). Den svarer til vinklen fra forårspunktet ^ til middelsolen M* på ekliptika
l m(t) = Ð ^ TM*
Tilsvarende definerer vi Solens sande længde til
l (t) = Ð ^ TP*
dvs. vinklen fra ^ til Solens tilsyneladende position P* på ekliptika.
De to indførte længder bringer Ptolemaios kun i spil, når han skal referere til observationer af Solen.
I forbindelse med mere teoretiske undersøgelser foretrækker han et andet par af længder, som henviser til apsidelinien TA* gennem solbanens apogæum A. Han indfører således
a(t) = Ð A*TP* = Ð ATP
som angiver vinklen fra apsidelinien TA* til Solens tilsyneladende sted P* - set fra Jorden. Da TP drejer sig med ujævn vinkelhastighed omkring T, bliver a(t) en voksende, men ikke lineær funktion af tiden. Den kaldes Solens sande anomali.
Den anden variabel i dette system er middelanomalien
am(t) = Ð ADP.
Den angiver Solens position P i sin excentriske bane. Da DP drejer med konstant vinkelhastighed, bliver am(t) en voksende, lineær funktion af tiden.
Vi ser, at positionen af middelsolen M* er koblet til Solens sande sted P på den måde, at Solens tilsyneladende sted P* aldrig ligger langt fra M*. Koblingen etableres ved, at TM altid er parallel med DP. Vi kan så definere centerækvationen
q = Ð M*TP = Ð TPD = l (t) - l m(t) = a(t) - am(t) ( 3)
Bemærk at q bliver negativ, når 0° < a < 180° , men positiv, når 180° < a < 360° . For Ptolemaios er q altid en positiv størrelse, som så veksler mellem at blive trukket fra eller lagt til am(t) for at give a(t).
Det fremgår umiddelbart, at q opfylder symmetribetingelsen
q(a) = -q(360° -a) eller q(am) = -q(360° -am) ( 4)
idet enhver situation har et modstykke symmetrisk i forhold til apsidelinien.
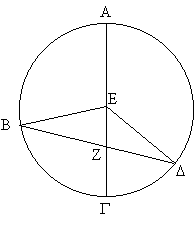 |
Mere overraskende er det, at der gælder
På Figur 5 fastholder vi Ptolemaios’ oprindelige betegnelser: Z er jordcentret, mens E er centrum for deferenten. Formel (5) udtrykker, at i en situation, hvor Solens tilsyneladende bue fra apogæum a = Ð AZB har en given værdi, vil centerækvationen være af samme størrelse, som i den situation, hvor Solens tilsyneladende bue fra perigæum Ð G ZD har samme værdi a. Ptolemaios’ bevis19 bygger på, at trekant EBD er ligebenet - længderne af både EB og ED er lig med radius i den excentriske cirkel. Derfor bliver de to vinkler Ð EBZ og |
Ð ED Z lige store; og disse vinkler angiver netop centerækvationen.
Med moderne matematiske metoder20 er det ganske enkelt at fastlægge størsteværdien af q(a). Vi kan anvende sinus relationen på trekant TDP på Figur 4
sin q = ![]() sin a
sin a
hvoraf
sin qmax = ![]()
for sin a = 1
Det betyder, at størrelsen af q er størst for de to positioner af Solen, hvor den sande anomali er 90° henholdsvis 270° - dvs. positionerne B og D på Figur 6.
Ptolemaios leverer et geometrisk bevis21, hvor han bringer Figur 6 i spil. Q angiver et punkt, for hvilket middelanomalien er mindre end for B.
Beviset går ud på at vise, at
Ð EBZ = q(B) > q(Q ) = Ð EQ Z
Beviset bygger på en sætning hos Euklid III, 7, hvor det bevises, at i tilfælde af, at Z er et punkt på
diameteren gennem A, uden for cirklens centrum E, vil afstanden ZQ stadig blive mindre og mindre, når Q bevæger sig længere og længere væk fra A.
| Det betyder, at der i trekant Q D Z gælder
og således
Der gælder
så ved addition får vi
|
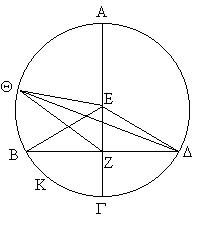 |
Men
Ð ED Z = Ð EBZ
så
Ð EBZ > Ð EQ Z
hvilket skulle bevises.
På tilsvarende måde beviser Ptolemaios, at også for et punkt K med større middelanomali end B vil gælde
Ð EBZ > Ð EKZ
Altså: den største værdi af vinkel q(a) forekommer i B eller D .
Ved præsentationen af ovenstående sætning22 nævner Ptolemaios den
overraskende kendsgerning, at det netop er i de to "kvadrant"-punkter B og D , at Solens vinkelhastighed ![]() er lig med dens middelhastighed w ¤ . Ptolemaios giver ikke noget bevis for påstanden;
men han har sandsynligvis indset det i forbindelse med praktisk arbejde med sine tabeller.
er lig med dens middelhastighed w ¤ . Ptolemaios giver ikke noget bevis for påstanden;
men han har sandsynligvis indset det i forbindelse med praktisk arbejde med sine tabeller.
Det er forholdsvis enkelt at indse, at påstanden er rigtig ved brug af moderne differentialregning.
Formel (3) kan omskrives
l (t) = l m(t) + q
Ved differentiation bliver det til
![]()
Leddet på venstre side af lighedstegnet er P*’ vinkelhastighed, mens første led på højre side er w ¤ . Da andet led på højre side bliver nul de steder, hvor q opnår sin størsteværdi (eller mindsteværdi), gælder
![]() = w
¤ ved a = 90° eller
a = 180°
= w
¤ ved a = 90° eller
a = 180°
som Ptolemaios påstår.
Opgaven går nu ud på at fastlægge værdier for parametrene R, e og l a i den excentriske model på en sådan måde, at den stemmer overens med observationer af Solens tilsyneladende bevægelse. Ptolemaios23 vælger at bygge på, at Hipparch i sin tid fandt
forårets længde til 94½ døgn
sommerens længde til 92½ døgn
Han regner også på sine egne observationer, som giver et lidt andet resultat. Alligevel fastholder han de 300 år gamle værdier.
På Figur 724 er Ptolemaios’ notation bevaret. Den viser ekliptika og den excentriske cirkel med centrum i henholdsvis E og Z. Ved forårsjævndøgn er Solens tilsyneladende sted ^ = A, mens den faktisk befinder sig i punktet Q i den excentriske bane. Tilsvarende er Solen ved sommersolhverv tilsyneladende i B på ekliptika, men i virkeligheden i K i sin bane, og positionen G ved efterårsjævndøgn svarer til L .
De buer, der er af interesse, findes nemt
Q K = 94½× w ¤ = 93° ; 9
KL = 92½× w ¤ = 91° ;11
Q K + KL = 181° ;20
L M Q = 175° ;40
Opgaven består derfor i at anbringe den excentriske cirkel indeni ekliptika på en sådan måde, at disse tre buer set fra Jorden projiceres ud på ekliptika som buer på 90° , 90° og 180° . Da foråret er den længste årstid, er det klart, at den længste fjerdedel på den excentriske cirkel skal anbringes i 1. kvadrant ABE på figuren. Gennem Z tegnes diametrene NO parallel med AG og PP parallel med BD . Vi kan så beregne de lige store buer NQ og OL ud fra
NQ + 180° + OL = Q K + KL = 184° ;20
hvoraf vi ser
NQ = O L = 2° ;10
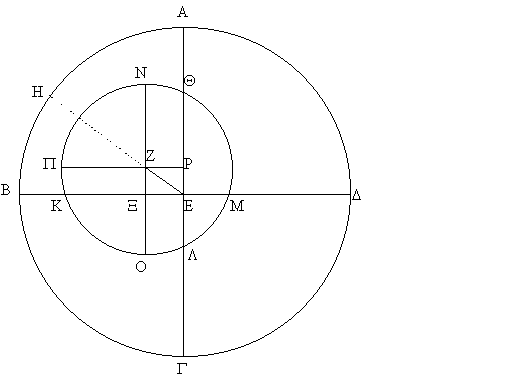 |
På samme måde finder vi P K = 93° ;9 - N Q - 90° = 0° ;59 Vi kan nu beregne PZ = 60p× sin 2° ;10 = 2p;16 og PE = 60p× sin 0° ;59 = 1p;2 hvor Ptolemaios har sat deferentens radius til den vilkårlige værdi R = 60p - sandsynligvis for at gøre det nemmere for ham at bruge sin kordetabel, som vi klarer os uden, fordi vi i stedet anvender trigonometriske funktioner. Det er nu nemt at finde excentriciteten samt apogæums beliggenhed på den excentriske cirkel. Ved hjælp af Pythagoras’ sætning får vi e = EZ = |
som er meget tæt på 60p/24. Så som excentricitet får vi
e/R = 1/24
Desuden gælder
sin l a = sin ZEP = PZ/ZE = (2p;16)/(2p;29,30)
dvs.
l a = 65° ;30
Resultatet stemmer naturligvis med Hipparchs. Undersøgelser25 tyder på, at det er en tilfældighed, at Hipparch ramte næsten plet, idet l a på hans tid kun afveg 3/4° fra 65° ;30, mens Solens apogæum i løbet af de 300 år frem til Ptolemaios’ tid må have flyttet sig godt 5° mod øst. Nøjagtigheden af deres bestemmelser af årstidernes længder har ikke kunnet sikre et præcist resultat26.
Når Ptolemaios skal beregne Solens position til et givet tidspunkt, vil han i første omgang bestemme dens middellængde ved hjælp af de tidligere nævnte tabeller. Når han så skal beregne forskellen
| mellem middellængden og den sande længde - dvs. centerækvationen q - er
det praktisk, at q beregnes som funktion af middelanomalien am. På forhånd ved vi, at q(0° ) = q(180° ) = 0° . Desuden ses på Figur 6, at sin qmax = 1/24, hvilket giver qmax = 2° ;23. Størsteværdien forekommer ved a(t) = 90° eller a(t) = 270° ; det vil sige ved am(t) = 93° ;23 eller ved am(t) = 267° ;37 27. For en given værdi af am kan q beregnes ved hjælp af Figur 8 28. Punktet K fastlægges ved at tegne den vinkelrette linie fra T på forlængelsen af PD. Vi får
Nu kan centerækvationen findes sin q(am) = hvor |
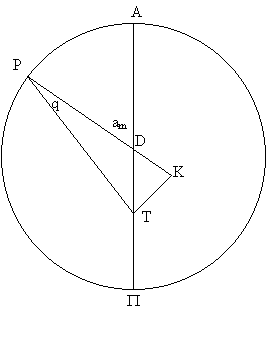 |
![]()
er afstanden mellem Solens centrum P og Jordens centrum T, når middelanomalien er am.
Det skal bemærkes, at Ptolemaios ikke benytter trigonometriske funktioner, men kordetabeller; han opstiller ikke funktionsudtryk, men tabeller. Sammen med de tidligere nævnte tabeller over Solens middelbevægelse - og en startværdi eller epoke - har Ptolemaios fuldført opgaven: Det er muligt at beregne Solens længde i ekliptika til et vilkårligt tidspunkt.