Solteorien hos Ptolemaios

Tilbage til indhold

Arbejde på et astronomihold

Vurdering af Ptolemaios’ tabeller

Jeg har sammenlignet resultatet i Ptolemaios’ tabel over centerækvationen²⁹ med en moderne beregning med trigonometriske funktioner. I stedet for de to foregående ligninger har jeg benyttet en simplere formel

( 6)

til beregning af a_m i Excel:

(omregning til grader og minutter er sket ved division af gradtallet med 24 og formatering af cellerne til klokkeslæt)

Afvigelserne er nogle få steder på sidste ciffer og skyldes nok afrundingen i Excel.

En moderne beregning af centerækvationen kan foregå ved f. eks. at benytte formler fra Strömgrens lærebog i astronomi³⁰. Det skal betænkes, at disse formler bygger på, at vinklerne regnes fra perigæum, mens Ptolemaios regner fra apogæum. Under den forudsætning får vi følgende materiale at arbejde med

E + e sin E = M [ 1]

                                    [ 2]

                                    [ 3]

e = 0,0167 [ 4]

hvor M angiver middelanomalien, E den excentriske anomali og v den sande anomali, mens e er den moderne værdi for excentriciteten i Jordens ellipsebane.

I Excel har jeg sammenlignet Ptolemaios’ q(a_m) fra formel (6) med M - v fra formel [3].

Resultatet er afbildet grafisk.

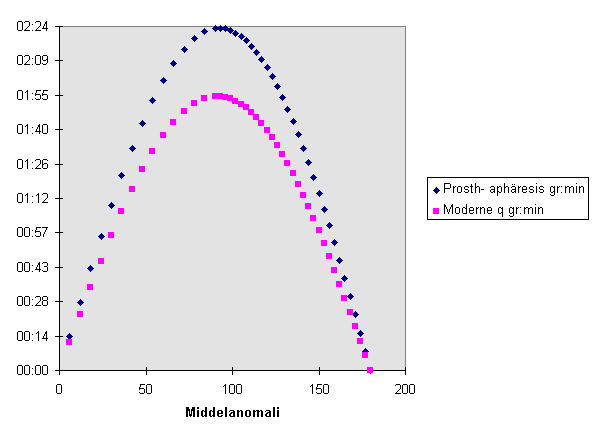
Det er markant, at Ptolemaios får for store værdier. Men tilsyneladende har de to kurver samme form. Beregner man den faktor, som de moderne værdier skal multipliceres med for at give Ptolemaios’ værdier viser det sig imidlertid, at den vokser jævnt fra 1,223 til 1,275, når middelanomalien ændres fra 6° til 177° . Men nedenfor er indlagt parabler som tendenslinier, og da ser vi, at de to sæt målepunkter ligger på en fælles usymmetriske måde.

Grafregneropgaver

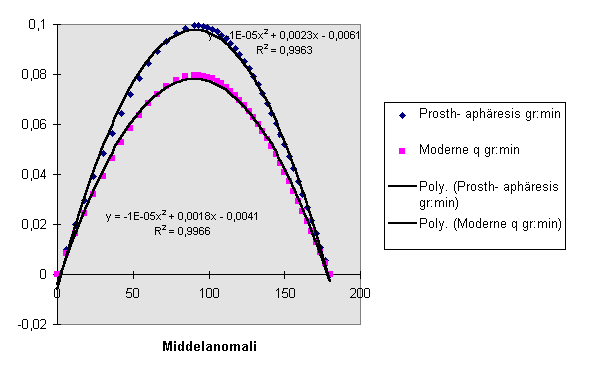
Siden Kepler opstillede sin 2. lov for planeternes bevægelse i deres ellipser, har astronomer kæmpet med opgaven: Beregn ud fra en given værdi for M den tilsvarende værdi for E - dvs. løs Keplers ligning. Ligningen er transcendent og løses altså ikke analytisk.

Men Solver funktionen på nutidens grafregner gør det nemt at løse ligningen - man skal blot være opmærksom på, at man skal regne vinklerne i radianer.

Følgende grafregnerprojekt, som udnytter Solver funktionen kan foreslås:

• Udfyld ved hjælp af (6) en tabel over q som funktion af a_m, og omregn til grader og bueminutter. Sammenlign med Ptolemaios’ tabel.
• Udfyld en tilsvarende tabel over E (radianer) som funktion af M (i grader) - [1].
• Udbyg den sidste tabel med v (i grader) som funktion af E [2].

Afslutning

I det foregående er der gennemgået en række problemstillinger, som har været centrale for Ptolemaios i hans arbejde, og som en gymnasieelev efter min mening kan overskue og følge løsningen af. Muligvis vil nogen mene, at problemstillingerne er lovlig matematisk præget; men frem til vor tid har astronomerne været tvunget til at udføre meget matematisk rutinearbejde - og det er vel passende at give eleverne et indtryk af det.

1. Man I side 182
2. Elis og Bengt Strömgren, Lærebog i Astronomi, Oslo 1945 side 137-138, 199-201

Tilbage til indhold